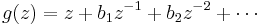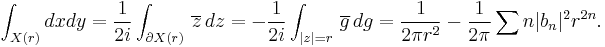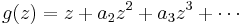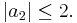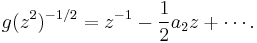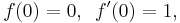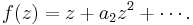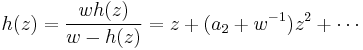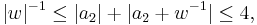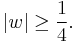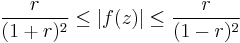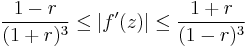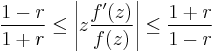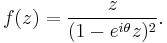Koebe quarter theorem

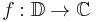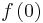In complex analysis, a branch of mathematics, the Koebe 1/4 theorem states that the image of an injective analytic function $f:\mathbb D\to\mathbb C$ from the unit disk $\mathbb D$ onto a subset of the complex plane contains the disk whose center is $f\,(0)$ and whose radius is 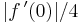$|f\,'(0)|/4$ . The theorem is named after Paul Koebe, who conjectured the result in 1907. The theorem was proven by Ludwig Bieberbach in 1914. The Koebe function ƒ(z) = z/(1 − z)² shows that the constant 1/4 in the theorem cannot be improved.

A related result is the Schwarz lemma, and a notion related to both is conformal radius.

1 Gronwall's area theorem
2 Bieberbach's coefficient inequality for univalent functions
3 Proof of quarter theorem
4 Koebe distortion theorem
5 Notes
6 References

Gronwall's area theorem

Suppose that

$g(z) = z %2Bb_1z^{-1} %2B b_2 z^{-2} %2B \cdots$

is univalent in 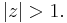$|z| > 1.$ Then

$\sum_{n\ge 1} n|b_n|^2 \le 1.$

In fact, if r > 1, the complement of the image of the disk |z| > r is a bounded domain X(r). Its area is given by

$\int_{X(r)} dxdy = {1\over 2i} \int_{\partial X(r)}\, \overline{z}\,dz = -{1\over 2i}\int_{|z|=r} \,\overline{g}\,dg={1\over 2\pi r^2} -{1\over 2\pi}\sum n |b_n|^2 r^{2n}.$

Since the area is positive, the result follows by letting r decrease to 1. The above proof shows quality holds if and only if the complement of the image of g has zero area, i.e. Lebesgue measure zero.

This result was proved in 1914 by the Swedish mathematician Thomas Hakon Gronwall.

Bieberbach's coefficient inequality for univalent functions

Let

$g(z) = z %2B a_2z^2 %2B a_3 z^3 %2B \cdots$

be univalent in 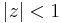$|z|<1$ . Then

$|a_2|\le 2.$

This follows by applying Gronwall's area theorem to the odd univalent function

$g(z^2)^{-1/2}= z^{-1} -{1\over 2} a_2 z %2B \cdots.$

Equality holds if and only if g is a rotation of the Koebe function.

This result was proved by Ludwig Bieberbach in 1916 and provided the basis for his celebrated conjecture that |a_n| ≤ n, proved in 1985 by Louis de Branges.

Proof of quarter theorem

Applying an affine map, it can be assumed that

$f(0)=0,\,\,\, f^\prime(0)=1,$

so that

$f(z) = z %2B a_2 z^2 %2B \cdots .$

If w is not in 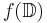$f(\mathbb D)$ , then

$h(z)={wh(z)\over w-h(z)} = z %2B(a_2%2Bw^{-1}) z^2 %2B \cdots$

is univalent in 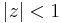$|z|<1$ .

Applying the coefficient inequality to f and h gives

$|w|^{-1} \le |a_2| %2B |a_2 %2B w^{-1}|\le 4,$

so that

$|w|\ge {1\over 4}.$

Koebe distortion theorem

The Koebe distortion theorem gives a series of bounds for a univalent function and its derivative. It is a direct consequence of Bieberbach's inequality for the second coefficient and the Koebe quarter theorem.^[1]

Let f(z) be a univalent function on |z| < 1 normalized so that f(0) = 0 and f'(0) = 0 and let r = |z|. Then

${r \over (1%2Br)^2}\le |f(z)|\le {r\over (1-r)^2}$

${1-r\over (1%2Br)^3} \le |f^\prime(z)| \le {1%2Br\over (1-r)^3}$

${1-r\over 1%2Br} \le \left|z{f^\prime(z)\over f(z)}\right| \le {1%2Br\over 1-r}$

with equality if and only if f is a Koebe function

$f(z) ={z\over(1-e^{i\theta}z)^2}.$

Notes

^ Pommerenke 1975, p. 21-22

References

Bieberbach, Ludwig (1916), Über die Koeffizienten derjenigen Polenzreihen, welche eine schlichte Abbildung des Einheitskreises vermitteln, pp. 940-955
Carleson, L.; Gamelin, T. D. W. (1993), Complex dynamics, Universitext: Tracts in Mathematics, Springer-Verlag, pp. 1-2, ISBN 0-387-97942-5
Duren, P. L. (1983), Univalent functions, Grundlehren der Mathematischen Wissenschaften, 259, Springer-Verlag, ISBN 0-387-90795-5
Gronwall, T.H. (1914), "Some remarks on conformal representation", Ann. of Math. 16: 72-76
Nehari, Zeev (1952), Conformal mapping, Dover, pp. 248-249, ISBN 0-486-61137-X
Pommerenke, C. (1975), Univalent functions, with a chapter on quadratic differentials by Gerd Jensen, Studia Mathematica/Mathematische Lehrbücher, 15, Vandenhoeck & Ruprecht
Rudin, Walter (1987). Real and Complex Analysis. Series in Higher Mathematics (3 ed.). McGraw-Hill. ISBN 0070542341. MR 924157.
Koebe 1/4 theorem at PlanetMath